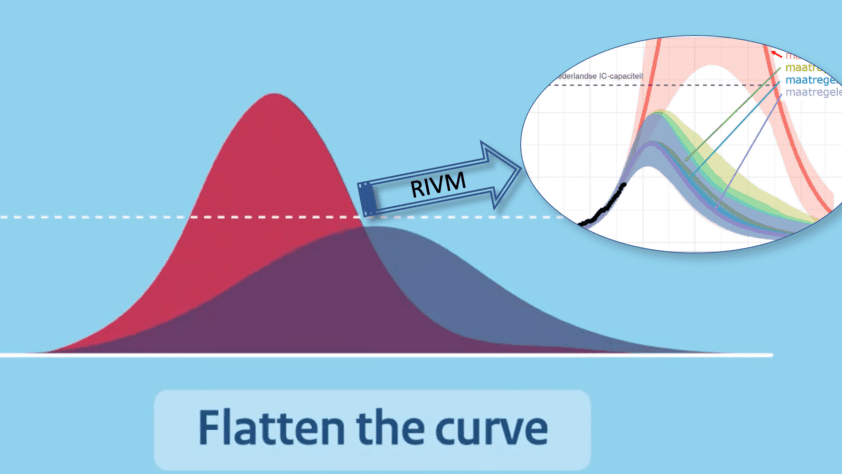
De grafieken die Van Dissel ons regelmatig presenteerde, bevatten telkens prognoses die altijd de grootst mogelijke bulten voorspelden. Ze waren telkens reden om strenge maatregelen in te voeren, die succesvol waren omdat de resultaten ervan niet te zien waren: de Preventieparadox. Maar wat was er dan mis met het RIVM-model?
Lees volledig artikel: Het RIVM-model ontmanteld
Prognoses
Na de uitbraak van corona heeft het RIVM regelmatig prognoses afgegeven over de verwachte ontwikkeling van de verspreiding van het virus, afhankelijk van de keuze van te nemen maatregelen. De betrouwbaarheid van deze prognoses heeft voortdurend onder vuur gelegen, maar er is nooit onderzoek gedaan naar de juistheid van het model.
Eind 2021 heeft het RIVM dit rapport gepubliceerd: Beschrijving transmissiemodel berekening zorgbelasting waarin het model wordt beschreven.
Laten we eerst eens kijken wat de wetenschap zegt over de verspreiding van een virus. Op de website van het RIVM staat een overzicht: “Rekenmodellen openbaar en toegankelijk”. Daarin vinden we o.a. een verwijzing naar een publicatie in maart 2020 in het zeer gerenommeerde wetenschappelijke tijdschrift The Lancet: How will country-based mitigation measures influence the course of the COVID-19 epidemic? van Anderson et al.
Laten we daar eerst eens naar kijken.
The Lancet
In dit wetenschappelijke artikel wordt aan de hand van een model, gebaseerd op de bekende eenvoudige rekenformules, via een simulatie getoond wat het effect zou kunnen zijn van maatregelen. Deze grafiek geeft hierin veel inzicht:

We zien hier drie lijnen. De rode lijn is het veronderstelde verloop van het aantal besmettingen van een epidemie met een reproductiegetal van 2 zonder maatregelen. Na bijna 4 maanden wordt de top van het aantal besmettingen bereikt. Dat komt overeen met het bereiken van de waarde van 1 voor het reproductiegetal R. De waarde van R wordt enerzijds bepaald door de besmettelijkheid van het virus en anderzijds door de opbouw van immuniteit door het doormaken van een infectie. Als de R0 (de R-waarde als nog niemand immuniteit bezit) de waarde 2 heeft, zoals in dit rekenvoorbeeld, dan is op de top precies de helft van de bevolking besmet geweest.
Nu gaan we kijken naar het effect van maatregelen. Eerst zien we een groene lijn. Die ontstaat bijvoorbeeld door afstandsmaatregelen (“social distancing”) zoals bij ons de 1,5m maatregel. Daardoor vermindert het aantal contacten tussen mensen en dus remt het de epidemie af met hier 50%. Maar de top blijft liggen op een R-waarde van 1, dus door de verminderde opbouw van immuniteit wordt de top van de curve een aantal weken uitgesteld. Maar het duurt ook een aantal maanden extra voordat de epidemie weer tot een acceptabel niveau is gedaald. Dat is het principe van “Flattening the curve”. Het totaal aantal mensen dat besmet zal worden, blijft vrijwel gelijk, maatregelen waren 50% succesvol.
Interessanter wordt de blauwe lijn. Daarin worden na bijna 3 maanden zeer strenge maatregelen genomen: lockdown, quarantaine, sluiten openbare gelegenheden etc. We zien dan ook een flinke daling vanaf dat moment. Na 6,5 maand worden in dit voorbeeld de maatregelen opgeheven en er volgt een tweede golf, waarin net zoveel mensen besmet zullen worden als bij de golf met alleen social distancing. Het grote verschil is natuurlijk dat we bij de groene lijn na 7 maanden vrijwel verlost zijn van het virus, maar bij de blauwe pas bij 12 maanden. Het principe van Flatten the curve!
De Nederlandse situatie past het beste bij het tweede scenario. Na een eerste golf die na enkele maanden in mei 2020 voorbij leek, ontstond een tweede golf in de herfst van 2020. Het artikel van Anderson beschreef dit al!

RIVM
De publicatie in The Lancet uit maart 2020 is dus voor het RIVM geen reden geweest om dit principe te erkennen. Er werd toch besloten tot strenge maatregelen, ondanks dat het verloop van de epidemie in april naadloos aansloot bij het beschreven model. Strenge maatregelen werden slechts in kleine stappen afgebouwd tot de zomer van 2020, dus een grotere tweede golf was het gevolg. Vrijwel exact gelijk aan het voorbeeld in de eerste grafiek!
Het principe was zeker wel bekend bij de PR afdeling van het RIVM, want in een Tweet van het RIVM wordt dit principe nog eens uitgelegd:
Bij een te snelle stijging van het aantal ernstig zieke mensen, raakt ons zorgsysteem overbelast. We hebben dan niet genoeg IC-bedden. Door ‘social distancing’ worden minder mensen tegelijk ziek en is er voldoende zorgcapaciteit. Dit noemen we ‘flatten the curve’. 🏥 #AlleenSamen pic.twitter.com/euDudBRdgS
— RIVM (@rivm) April 6, 2020
Ook hier zien we bij de RIVM tweet het principe dat maatregelen zowel de hoogte van de top halveren als de duur van de epidemie verdubbelen. Flatten the curve . In een artikel van Wallinga et al wordt dit principe nog eens bevestigd!
Hoe anders zijn de grafieken die het RIVM ons toonde om het beoogde effect van maatregelen te suggereren. Elke maand werden er wel één of twee grafieken getoond die dezelfde structuur hadden. Een voorbeeld van 25 oktober 2020:
 We zien hier vier scenario’s die het RIVM met elkaar vergelijkt. Rood het meest soepele: alleen de maatregelen van 28 september. Blauw het meest strenge scenario: een strenge lockdown met o.a. alle scholen dicht. We hebben hierboven gezien dat hoe strenger de maatregelen zijn, hoe lager de top (dat is ook inderdaad wat we hier zien) maar ook hoe breder de golf zich gaat uitstrekken. Hier zien we juist het tegenovergestelde effect. Strengere maatregelen zorgen juist voor een verkorting van de duur van de epidemie en dat gaat in tegen alle basisregels zoals ook beschreven in het artikel van The Lancet.
We zien hier vier scenario’s die het RIVM met elkaar vergelijkt. Rood het meest soepele: alleen de maatregelen van 28 september. Blauw het meest strenge scenario: een strenge lockdown met o.a. alle scholen dicht. We hebben hierboven gezien dat hoe strenger de maatregelen zijn, hoe lager de top (dat is ook inderdaad wat we hier zien) maar ook hoe breder de golf zich gaat uitstrekken. Hier zien we juist het tegenovergestelde effect. Strengere maatregelen zorgen juist voor een verkorting van de duur van de epidemie en dat gaat in tegen alle basisregels zoals ook beschreven in het artikel van The Lancet.
Bovendien zouden de maatregelen ook een einddatum moeten hebben en die maakt geen deel uit van de prognose. Als we te maken zouden hebben met de blauwe lijn uit de grafiek van The Lancet en op zeg 1 februari de maatregelen opgeheven zouden worden, dan zou bij een kloppend model een “rode bult” te zien moeten zijn. De opbouw van immuniteit is immers een halt toegeroepen en zal daarna zorgen voor een uitgestelde bult. Als het RIVM zich hiervan bewust was geweest, had dit in het model zichtbaar gemaakt moeten worden! Het feit dat dit verzwegen werd, getuigt van hetzij het ontbreken van basaal inzicht in de verspreidingsprincipes, dan wel het bewust verkeerd voorlichten van de regering.
De werkelijkheid werd dat de bezetting van de IC kort na het verschijnen van deze prognose daalde tot onder de 200 medio november.
Het RIVM model
Deze merkwaardige voorspellingen, waarvan de uitkomst dus strijdig is met de natuurwetten, komen uit een model waarvan de code nog steeds niet openbaar is, ondanks berichten hierover dat het wel zo zou zijn. Echter, elke informaticus zal beamen dat het doorgronden van door anderen geschreven software vrijwel onmogelijk is, zonder een duidelijke beschrijving van de programma regels. Daarnaast zitten er kennelijk fouten in de code, die tot deze onbestaanbare grafieken leiden. Kennelijk zelfs voor de bouwers van de code ondoenlijk deze fouten op te sporen en reden om geen vervolg publicaties meer te schrijven.
Laten we ons beperken tot de analyse van het artikel dat het model beschrijft. Het is een voorlopige versie van 8 december 2021, waarvan geen bijgewerkte versies te vinden zijn. Het RIVM zegt daar dat het model is bedoeld om de bezetting van het ziekenhuis te voorspellen, het effect van maatregelen en het weglaten daarvan. Het beperken van mobiliteit staat daarbij centraal.
Het RIVM gaat uit van een SEIR model, aangevuld met een “apart compartiment voor vaccinatie” en het ook weer verliezen van deze immuniteit (pagina 2).
Immuniteit wordt in dit model bepaald door de Pienter-Corona studie (pagina 3) en dat is merkwaardig. Metingen vormen dus een onderdeel van dit model. Je zou deze als startwaarde kunnen gebruiken, maar het bepalen van immuniteit door het meten van antistoffen is een hachelijke zaak. Als je gebruik maakt van een model waarin (de opbouw van) immuniteit de belangrijkste drijvende kracht is, dan moet je erg zeker zijn van het juist kunnen bepalen van de immuniteit. Antistoffen verdwijnen na verloop van tijd weer uit het bloed, dus die cijfers zijn feitelijk onbruikbaar!
Verspreiding van het virus wordt verder gedaan via een model van Wallinga et al (september 2013), waarin de verspreiding van influenza wordt beschreven. Seizoen en luchtvochtigheid zijn daarin de belangrijkste factoren, die overigens ook het langste door het RIVM zijn ontkend. Ook is opgebouwde immuniteit volgens dat artikel een belangrijke factor. Merkwaardig. Groepsimmuniteit is inmiddels not done, immuniteit kan volgens WHO voortaan alleen bereikt worden door vaccinatie, dus de vraag is wat dat dan voor het model betekent.
Immuniteit wordt binnen het model bepaald op basis van een VE volgens de literatuur (pagina 6) en dat bepaalt hoeveel vatbare mensen er in elke leeftijdsgroep immuun worden. Het wordt dus niet gestuurd door de opbouw van natuurlijke immuniteit, die wel onderdeel vormt van het SEIR-model dat volgens pagina 1 wordt gebruikt. Alweer merkwaardig. Ook wordt gesteld dat “Een onderliggende aanname is dat het vaccin volgens een alles-of-niets manier werkt: na vaccinatie is de gevaccineerde of volledig vatbaar of volledig immuun.”
De uitkomst van het model wordt vervolgens gefit met het aantal IC-opnames. Het aantal IC-opnames goed in beeld krijgen door het model is dus een primair doel.
De beschrijving van het model staat dus vol tegenstrijdige aannames.
Validiteit van het model
Op pagina 9 wordt gesproken over de validiteit van het model. Het RIVM geeft daarin toe dat het model alleen gevalideerd is voor het beschrijven van de eerste golf. De maatregelen werden pas ingezet toen de golf al over de top was (achteraf te constateren). Het RIVM schrijft daarover o.a.:
Het is immers niet mogelijk de validiteit en betrouwbaarheid van verschillende hypothetische scenario’s te beoordelen, aangezien deze scenario’s nooit tegelijkertijd werkelijkheid kunnen worden. En vaak zelfs niet één van de scenario’s de werkelijkheid wordt, bijvoorbeeld doordat maatregelen in de tussentijd worden aangepast. En dus kunnen de uitkomsten van deze hypothetische scenario’s in de praktijk niet achteraf met elkaar vergeleken worden.
Wat je wel van een wetenschappelijke organisatie mag verwachten, is enige zelfreflectie. Op zijn minst mag je van een model verwachten dat de uitkomsten voldoen aan het “Flatten the curve” principe, dus dat door het vertragen van de verspreiding niet alleen de belasting van de ziekenhuizen wordt verlaagd, maar ook dat de daarvoor te betalen prijs is dat de epidemie ook vertraagd wordt, dus langer duurt. De vraag die daaraan onlosmakelijk verbonden is, dat is de vraag wat het dan betekent dat een maatregel een effect heeft van bijvoorbeeld 10%. Kennelijk zit er in het hoofd van iedereen die zich met het modelleren bezighoudt (en daarmee ook de politici en andere beleidsmakers) dat een 10% effect betekent dat er ook 10% minder IC-opnames zijn. En dat is dus een foute veronderstelling.
Marion Koopmans sprak in dat verband over de preventieparadox. Hierover schreven wij een artikel, dat het mechanisme uitlegt aan de hand van het SEIR-model: De paradox van de maatregelen waarin we uitleggen dat de maatregelen een in de tijd verschuivend effect hebben, precies zoals Anderson ook beschrijft in The Lancet.
De broncode
Er wordt ook gesproken over het beschikbaar komen van de broncode. Al eerder stelden wij dat het vrijwel ondoenlijk zou zijn om deze code te begrijpen en ook werkend te krijgen op een eigen computersysteem.
Wel wordt er aan het eind van het artikel een opsomming van een aantal formules gegeven, die samen het model vormen. We hebben de code dus niet kunnen vinden op github.com! RIVM lijkt aan te geven dat er door personeelstekorten keuzes gemaakt moesten worden en er daarom ook geen “dummy data” beschikbaar is voor evaluatie.
Te veel knoppen?
We zien aan de ene kant dat het model altijd voorspellingen doet (Van Dissel noemt het inmiddels “slechts scenario’s”) die structureel veel te hoge waarden opleveren. Aan de andere kant zien we ook dat de processen als “groepsimmuniteit” en “Flatten the Curve” niet worden teruggevonden in de cijfers. Het model wekt hiermee de schijn van een monster met te veel knoppen, waarvan niemand meer het overzicht heeft. Mogelijke software fouten kunnen ook een oorzaak zijn voor het falen van het model.
Het model van het Green Team heeft slechts twee “knoppen”: de initiële waarde van het reproductiegetal en het aantal mensen dat inmiddels immuniteit heeft gekregen. Beide cijfers weten we niet, maar kunnen wel goed geschat worden aan de hand van de cijfers uit het verleden. Dit is een actueel voorbeeld:

Hier zien we de prognose voor het verloop van de BA.5 golven. De precieze prognose kon pas gegeven worden nadat de seizoensinvloed verscheen. De exacte datum van dat meteorologisch aspect was door ons niet te voorspellen, maar zodra zich dat manifesteerde, kon het verwerkt worden in de prognose. Aardig is het om te zien dat er inmiddels weer een opleving is, waarschijnlijk als gevolg van de kortgeleden opgedoken CH.1.1 variant. Deze parameter kennen we nog onvoldoende om een goede prognose af te geven. Wel zien we dat het model gebaseerd op de klassieke formules uitstekend het verloop weet te beschrijven. Een eenvoudig tweetal formules in een Excel spreadsheet….
Conclusies
Het RIVM-rapport beschrijft de rekenwijze van het RIVM-model, dat prognoses oplevert voor het verloop van de epidemie. Er werd al langer getwijfeld aan de juistheid van dit model. Een validatie van de code is helaas niet mogelijk, maar wel kunnen we vaststellen dat het model niet voldoet aan het gedrag zoals beschreven in het artikel waar het rapport naar verwijst: “Flatten the curve”. Dat is de sterkste aanwijzing dat er fundamentele fouten in het model zitten. Ook publicaties van Wallinga laten zien dat het totaal aantal besmettingen niet verandert, dus des te merkwaardiger dat we dit niet terugvinden in de grafieken van het rekenmodel waar Wallinga zijn naam aan heeft verbonden.
Het rapport spreekt van een “voorlopige versie van 8 december 2021” maar een definitieve versie is voor zover ons bekend niet verschenen. Ook geen peer-reviewed artikel waarin het model op wetenschappelijke wijze beschreven wordt. De grote vraag is daarmee: is het beleid van de Nederlandse overheid wel gebaseerd op wetenschap of was het alleen politiek?