De Engelse variant van het covid-19 virus krijgt volop aandacht en het OMT jaagt ons bij monde van Rutte en De Jonge flink schrik aan. Er worden allerlei cijfers genoemd, maar wat leren we daar nu van? Zijn de cijfers juist, en zijn ze aannemelijk? Wij proberen de zaak hier op een rijtje te zetten
Lees volledig artikel: De Engelse variant, wat leren de cijfers?
R-waarde
Elk virus wordt gekenmerkt door het reproductiegetal R; elke Nederlander heeft er wel van gehoord en kan er mee rekenen zodra die de waarde 2 heeft, want dan weten we dat 1 persoon er 2 besmet, 2 besmetten er 4 enzovoorts.
Eigenlijk moeten we spreken van een R0-waarde, dat is de R-waarde die het virus heeft zonder maatregelen en wanneer nog niemand anders besmet is geweest. Voor covid-19 is dat ongeveer 2,5 en het virus neemt er dan 4 dagen de tijd voor om 2,5 anderen te besmetten. Zo weten we ook hoe snel het virus zich verspreidt, want na 12 dagen zijn er dan 2,5 X 2,5 X 2,5 = (afgerond) 16 mensen besmet. Enzovoorts.
Gedurende het verloop van de epidemie gaan we spreken over de effectieve R-waarde: Reff, die steeds kleiner wordt, omdat er immuniteit wordt opgebouwd. Het doel van maatregelen is de Reff nog verder te verlagen, omdat het streven is deze verder onder de 1 te krijgen. Dan dooft de epidemie sneller uit.
Extra besmettelijk
Er kan niet over de Engelse variant gesproken worden, of de woorden extra besmettelijk maken onderdeel uit van de zin. Maar wat wordt hier eigenlijk mee bedoeld? Word je er zieker van of sneller ziek? Of grijpt het juist sneller om zich heen? Neemt het de plaats in van het originele virus? Wat is het?
De Engelse variant heeft een iets gewijzigde DNA structuur, waardoor zijn eigenschappen ook iets zijn veranderd. Wat de gevolgen daarvan zijn is nog steeds niet duidelijk, maar het zal gevolgen hebben voor de R0 waarde en mogelijk ook voor de dodelijkheid van deze variant. Meestal wordt een virus zwakker als het gemuteerd is, maar dat is hier nog niet vastgesteld.
We concentreren ons hier op de veranderde R0 waarde. Die is bijna per definitie groter dan de R0 van de originele covid-19, want als deze lager was, dan was de variant uitgestorven.
Het feit dat de R0 van de variant hoger is dan die van het oorspronkelijke covid-19 virus, wordt uitgedrukt als een percentage extra besmettelijkheid. Dat percentage is het deel van de R0 van de variant dat hoger is dan de R0 van het oorspronkelijke Covid-19 virus.
Samengesteld reproductiegetal
Maar wat als de variant en het oorspronkelijk virus tegelijk aanwezig zijn? Vooropgesteld dat het immuunsysteem van de mens deze beide herkennen en de opgebouwde immuniteit ook werkt voor de mutant, dan mag je de R-waarden bij elkaar optellen, maar dan wel gewogen naar het aandeel dat beide hebben. Het aandeel van de variant neemt toe in de tijd, dus zal ook de samengestelde R variëren in de tijd en wel voortdurend toenemen. Bijvoorbeeld van 0,8 als de variant nog vrijwel afwezig is tot 1,2 als er alleen de variant overgebleven is.
Dat moet je dan nog wel even netjes uitrekenen, maar er is dus een vast verband tussen de toename van het aandeel van de variant en de verhoging van de R-waarde.
Bovendien is er ook iets te zeggen over de tijd dat de variant al in Nederland is!
Maatregelen
Wat voor effect hebben maatregelen op de Engelse variant? In principe hebben maatregelen voor beide varianten hetzelfde effect. Als een maatregel in staat is om de actuele R-waarde omlaag te brengen, zal dat voor beide varianten evenveel effect hebben. Het zal vrijwel geen effect hebben om de groei van het aandeel van de Engelse variant te stoppen. Alleen de piek van de epidemie wordt iets verlaagd (flatten-the-curve).
Hoe lang is de Engelse variant al aanwezig?
Als we weten wat de extra besmettelijkheid is en ook in welke verhouding op een gegeven datum de variant aanwezig is, kunnen we een grove schatting maken wanneer het virus is overgestoken van Engeland naar Nederland (als dat de route geweest is). Dat kan, omdat we weten hoeveel mensen er nu besmet zijn (ongeveer 100.000) en hoe lang het duurt voordat 1 persoon voor zoveel besmetting heeft gezorgd dat er nu ongeveer 10.000 mensen met deze variant rondlopen. Stel bijvoorbeeld dat de individuele R-waarde van de variant 1,4 zou zijn, dan besmet 1 persoon er 1,4; na 4 dagen zijn dat er dan 2. Dus een verdubbeling in 8 dagen. Dan is uit te rekenen dat het ongeveer 105 dagen duurt (13 verdubbelingen) voordat 1 besmetting tot 10.000 besmettingen leidt. Bij een extra besmettelijkheid van 20% is dat dus ongeveer 210 dagen.
Het zal niet zo zijn dat een enkel persoon het virus naar Nederland heeft overgebracht, maar het is ook onwaarschijnlijk dat vele honderden personen daarvoor verantwoordelijk zijn geweest. Laten we er gemakshalve van uitgaan dat het er 10 geweest zijn, het gaat ook om een grove schatting! Besef ook dat er op het moment dat de eerste besmetting in Nederland plaatsvond, er in Engeland ook nog geen variant was waargenomen!
Scenario’s
Op een paar momenten is het aandeel van de variant gemeten:
- 11% aandeel. Onderzoek Twente
- 11,9% aandeel. Onderzoek RIVM week 1.
- 20-26% aandeel. Onderzoek Frankrijk
De metingen 11%, 11,9% en 20-26% aandeel gebruiken we om te toetsen of ons model plausibel is.
Er zijn in de loop van de tijd verschillende percentages genoemd, waarmee de Engelse variant besmettelijker zou zijn. Van klein naar groot zijn dit:
- 15% besmettelijker. Onderzoek Denemarken
- 20% besmettelijker. Onderzoek België
- 30% besmettelijker. Eerste schatting RIVM
- 35-40% besmettelijker. Laatste schatting RIVM
- 49% besmettelijker. Voorlaatste schatting RIVM
- 65% besmettelijker. Schatting Prof. Van Ranst (België)
Voor elk van deze scenario’s voor besmettelijkheid kunnen we berekenen wat op 12 februari de samengestelde R-waarde en aandeel zou moeten zijn, uitgaande van de gemeten R op 1 januari van 0,95 en dat het aandeel van de Engelse variant volgens het RIVM toen 5% zou zijn. Ook is dan terug te rekenen rond welke datum de B.1.1.7 ons land (virtueel) zou moeten zijn binnengekomen:
| Extra besmettelijkheid | R sameng. 12-02 | Aandeel 12-02 | Datum 1e besmetting |
|---|---|---|---|
| 15% | 0,92 | 17% | 1 juni 2020 |
| 20% | 0,93 | 23% | 1 juli 2020 |
| 30% | 0,98 | 39% | 15 september 2020 |
| 37,5% | 1,04 | 52% | 1 oktober 2020 |
| 49% | 1,14 | 70% | 1 november 2020 |
| 65% | 1,30 | 86% | 15 november 2020 |
| 18% * | 0,96 | 46% | 1 augustus 2020 |
Van deze scenario’s vallen de laatste drie (37,5%-65%) af, omdat we dan al een significante stijging van de samengestelde R-waarde hadden moeten zien. De actuele observaties falsificeren de twee meest recente schattingen van het RIVM! Dat wil zeggen, dat uit de metingen blijkt dat de RIVM schattingen er naast zaten.
Bij het eerste scenario zou het virus onwaarschijnlijk vroeg naar Nederland moeten gekomen zijn, om op 1 januari 2021 zo’n groot aandeel gehad te kunnen hebben en zou ook de R niet gestegen zijn vanaf 1 januari en dat zien we niet terug bij de observatie van de werkelijkheid.
De 20% en 30% scenario’s zijn plausibel en passen bij het verloop van de epidemie zoals we die observeren. Het virus zou dan dus ergens tussen juli tot september naar Nederland gekomen moeten zijn, aan het eind van de zomer dus.
Onze prognose op basis van cijfers in de praktijk
We hebben hierboven bepaald welke schattingen van het RIVM en elders plausibel zijn, maar we denken nog preciezer te kunnen zijn met ‘curve-fitting’, een gebruikelijke methode, in de statistiek om zo veel mogelijk in de buurt van de observaties te blijven. Het RIVM heeft deze methode regelmatig in het verleden toegepast maar doet dit momenteel, vreemd genoeg, in het geval van B117 niet.
Een extra besmettelijkheid van 18% past nog iets beter bij de kromming van de curve. Verder lijkt met name het aandeel B117 per 1 januari 2021 van invloed. Het RIVM heeft geen actuele meetgegevens van het aandeel B117, en haar meetgegevens van december/begin januari hebben een grote onzekerheid. Wel kunnen we proberen alternatieve waarden in het model in te vullen en te zien of de ontstane voorspelling past bij de waargenomen lichte groei sinds 1 januari van de R-waarde. Het blijkt dat als we kiezen voor een aandeel van 15% op 1 januari 2021, de curve het beste past. Die 15% valt binnen de onzekerheidsmarges van de waarde die het RIVM in week 1 heeft gemeten: 11,9% en is ook geheel in lijn met het gemeten aandeel B117 elders in Europa (11% in week 1 en 20-26% recent voor Frankrijk). Het is erg onaannemelijk dat Nederland exceptioneel zou afwijken qua aandeel B117 van de rest van Europa, zoals het RIVM dat stelt.
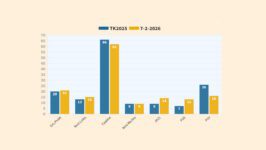
In de onderstaande figuur wordt het 18% scenario getoond, samen met wat de 35% prognose van het RIVM in de presentatie van 17 januari voor beeld had moeten tonen.

Conclusie
Bij gebrek aan betrouwbare metingen van het aandeel B117 moeten wij net als het RIVM afgaan op modellen, maar het verschil met het RIVM-model is dat onze curve wel de werkelijke opnamecijfers volgt. Onze prognose is empirisch gegrond op basis van actuele waarnemingen en meer in lijn met de rest van Europa en daarom in onze ogen aannemelijker dan de RIVM methode.
Samenvattend levert ons model de volgende kengetallen op:
- 18% Besmettelijker;
- 15% Aandeel op 1 januari;
- 46% Aandeel op 12 februari;
- de variant is waarschijnlijk naar Nederland gekomen in augustus 2020;
- geen exponentiële groei (maximum R is ongeveer gelijk aan 1 eind februari).
In dit model is de invloed van het naderende voorjaar niet meegenomen. Verwacht mag daarom worden, dat de R=1 niet bereikt zal worden, maar gedurende de maand maart net zoveel zal dalen, als het bij het aanbreken van de herfst is gestegen: ongeveer 20%.